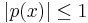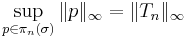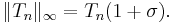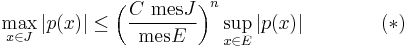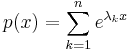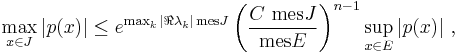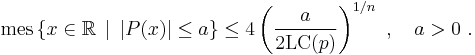Remez inequality
In mathematics, the Remez inequality, discovered by the Ukrainian mathematician Evgeny Yakovlevich Remez (Remez 1936), gives a bound on the sup norms of certain polynomials, the bound being attained by the Chebyshev polynomials.
Contents |
The inequality
Let σ be an arbitrary fixed positive number. Define the class of polynomials πn(σ) to be those polynomials p of the nth degree for which
on some set of measure ≥ 2 contained in the closed interval [−1, 1+σ]. Then the Remez inequality states that
where Tn(x) is the Chebyshev polynomial of degree n, and the supremum norm is taken over the interval [−1, 1+σ].
Observe that Tn is increasing on ![[1, %2B\infty]](/2012-wikipedia_en_all_nopic_01_2012/I/1c34f505a7068e8c4234753fb042ee87.png) , hence
, hence
The R.i., combined with an estimate on Chebyshev polynomials, implies the following corollary: If J ⊂ R is a finite interval, and E ⊂ J is an arbitrary measurable set, then
for any polynomial p of degree n. Here C>0 is a numerical constant.
Extensions
Inequalities similar to (*) have been proved for different classes of functions, and are known as Remez-type inequalities. One important example is Nazarov's inequality for exponential sums (Nazarov 1993):
Let
be an exponential sum (with arbitrary λk ∈C), and let J ⊂ R be a finite interval, E ⊂ J — an arbitrary measurable set. Then
where C>0 is a numerical constant.
In the special case when λk are pure imaginary and integer, and the subset E is itself an interval, the inequality was proved by Pál Turán and is known as Turán's lemma.
Pólya inequality
One of the corollaries of the R.i. is the Pólya inequality, which was proved by George Pólya (Pólya 1928), and states that the Lebesgue measure of a sub-level set of a polynomial p of degree n is bounded in terms of the leading coefficient LC(p) as follows:
References
- Remez, E. J. (1936). "Sur une propriété des polynômes de Tchebyscheff". Comm. Inst. Sci. Kharkow 13: 93–95.
- Bojanov, B. (May 1993). "Elementary Proof of the Remez Inequality". The American Mathematical Monthly (Mathematical Association of America) 100 (5): 483–485. doi:10.2307/2324304. JSTOR 2324304.
- Nazarov, F. (1993). "Local estimates for exponential polynomials and their applications to inequalities of the uncertainty principle type". Algebra i Analiz 5 (4): 3–66.
- Pólya, G. (1928). "Beitrag zur Verallgemeinerung des Verzerrungssatzes auf mehrfach zusammenhängende Gebiete". Sitzungsberichte Akad. Berlin: 280–282.